CSIR NET Physics JUNE 2023 Problem and answer

Physics INK
28 Dec, 2023

CSIR NET Physics JUNE 2023

Part A (Any 15)

Q1

Twenty litres of rainwater having a 2.0 μmol/L concentration of sulfate ions is mixed with forty litres water having 4.0 μmol/L sulfate ions. If 50% of the total water evaporated, what would be sulfate concentration in the remaining water 

  1. 3 μmol/L     
  2. 3.3 μmol/L     
  3. 4 μmol/L     
  4. 6.7 μmol/L✅

Q2

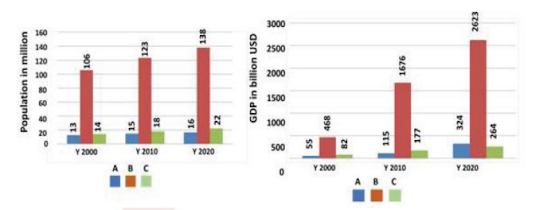
The populations and gross domestic products (GDP) in billion USD of three countries A, B and C in the years 2000, 2010 and 2020 are shown in the two figures below.
The decreasing order of per capita GDP of these countries in the year 2020 is 
  1.  A,B,C✅
  2. A,C,B
  3. B,C,A
  4. C,A,B

Q3

In a buffet, 4 curries A, B, C and D were served. A guest was to eat any one or more than one curry, but not the combinations having C and D together. The number of options available for the guest were
  1. 3✅
  2. 7
  3. 11
  4. 15

Q4

Three friends having a ball each stand at the three corners of a triangle. Each of them throws her ball independently at random to one of the others, once. The probability of no two friends throwing balls at each other is
  1. 1/4✅
  2. 1/8
  3. 1/3
  4. 1/2

Q5

What is the largest number of father-son pairs that can exist in a group of four men?
  1. 3✅
  2. 2
  3. 4
  4. 6

Q6

At a spot S en-route, the speed of a bus was reduced by 20% resulting in a delay of 45 minutes. Instead, if the speed were reduced at 60 km after S, it would have been delayed by 30 minutes. The original speed, in km/h, was
  1. 90
  2. 80
  3. 70
  4. 60✅

Q7

If the sound of its thunder is heard 1s after a lightning was observed, how far away (in m) was the source of thunder/lightning from the observer (given, speed of sound `=xms^(-1)` , speed of light `=yms^(-1)` )?
  1. `x^2/y`
  2. `(xy)/(y-x)`✅
  3. `(xy)/(x-y)`
  4. `y^2/x`

Q8

If two trapeziums of the same height, as shown below, can be joined to form a parallelogram of area `2(a+b)` , then the height of the parallelogram will be

  1. 4
  2. 1✅
  3. 1/2
  4. 2

Q9

Three fair cubical dice are thrown, independently. What is the probability that all the dice read the same?
  1. 1/6
  2. 1/36✅
  3. 1/216
  4. 13/216

Q10

Consider two datasets A and B, each with 3 observations, such that both the datasets have the same median. Which of the following MUST be true?
  1. Sum of the observations in A = Sum of the observations in B.
  2. Median of the squares of the observations in A = Median of the squares of the observations in B. 
  3. The median of the combined dataset = median of A + median of B.
  4. The median of the combined dataset = median of A✅

Q11

Price of an item is increased by 20% of its cost price and is then sold at 10% discount for Rs. 2160. What is its cost price?
  1. 1680
  2. 1980
  3. 1700
  4. 2000✅

Q12

A 50 litre mixture of paint is made of green, blue, and red colours in the ratio 5:3:2. If another 10 litre of red colour is added to the mixture, what will be the new ratio?
  1. 5:2:4
  2. 4:3:2
  3. 2:3:5
  4. 5:3:4✅

Q13

Two semicircles of same radii centred at A and C, touching each other, are placed between two parallel lines, as shown in the figure. The angle BAC is
  1. `30^circ`✅
  2. `35^circ`
  3. `45^circ`
  4. `60^circ`

Q14

A building has windows of sizes 2, 3 and 4 feet and their respective numbers are inversely proportional to their sizes. If the total number of windows is 26, then how many windows are there of the largest size?
  1. 4
  2. 6✅
  3. 12
  4. 9

Q15

Three consecutive integers `a,b,c` add to 15. Then the value of `(a-2)^2+(b-2)^2+(c-2)^2` would be 
  1. 25
  2. 27
  3. 29✅
  4. 31

Q16

Persons A and B have 73 secrets each. On some day, exactly one of them discloses his secret to the other. For each secret A discloses to B in a given day, B discloses two secrets to A on the next day. For each secret B discloses to A in a given day, A discloses four secrets to B on the next day. The one who starts, starts by disclosing exactly one secret. What is the smallest possible number of days it takes for B to disclose all his secrets?
  1. 5✅
  2. 6
  3. 7
  4. 8

Q17

Given only one full 3 litre bottle and two empty ones of capacities 1 litre and 4 litres, all ungraduated, the minimum number of pouring required to ensure 1 litre in each bottle is
  1. 2
  2. 3✅
  3. 4
  4. 5

Q18

Sum of all the integral angles of a regular octagon is ____________ degrees
  1. 360
  2. 1080✅
  3. 1260
  4. 900

Q19

Which of the numbers `A=162^3+327^3` and `B=612^3-123^3` is divisible by 489?
  1. Both A and B ✅
  2. A but not B 
  3. B but not A 
  4. Neither A nor B

Q20

When a student in Section A who scored 100 marks in a subject is exchanged for a student in Section B who scored 0 marks, the average marks of the Section A falls by 4, while that of Section B increases by 5. Which of the following statements is true? 
  1. A has the same strength as B 
  2. A has 5 more students than B ✅
  3. B has 5 more students than A 
  4. The relative strengths of the classes cannot be assessed from the data

Part B (Any 20)

Q1

A jar J1 contains equal number of balls of red, blue and green colours, while another jar J2 contains balls of only red and blue colours, which are also equal in number. The probability of choosing J1 is twice as large as choosing J2. If a ball picked at random from one of the jars turns out to be red, the probability that it came from J1 is
  1. 2/3
  2. 3/5
  3. 2/5
  4. 4/7✅

Q2

The Hamiltonian of a two-dimensional quantum harmonic oscillator is `H=p_x^2/(2m)+p_y^2/(2m)+1/2momega^2x^2+2momega^2y^2` where `m` and `omega` are positive constants. The degeneracy of the energy level `27/2cancel(h)omega` is
  1. 14
  2. 13
  3. 8
  4. 7 ✅

Q3

A uniform circular disc on the xy -plane with its centre at the origin has a moment of inertia `I_0` about the x -axis. If the disc is set in rotation about the origin with an angular velocity `baromega=omega_0(hatj+hatk)` , the direction of its angular momentum is along
  1. `-hati+hatj+hatk`
  2. `-hati+hatj+hatk`
  3. `hatj+2hatk` ✅
  4. `hatj+hatk`

Q4

A DC motor is used to lift a mass M to a height h from the ground. The electric energy delivered to the motor is `VIt` , where V is the applied voltage, I is the current and t the time for which the motor runs. The efficiency e of the motor is the ratio between the work done by the motor and the energy delivered to it. If `M=2.00pm0.02` kg, `h=1.00pm0.01`m, `V=10.0pm0.1` V, `I =2.00pm0.02` A and `t=300pm15` s, then the fractional error `|(dele)/e|` in the efficiency of the motor is closest to
  1. 0.05 ✅
  2. 0.09
  3. 0.12
  4. 0.15

Q5

A particle in one dimension is in an infinite potential well between `-L/2<=x<=L/2` . For a perturbation `epsilon cos((pix)/L)`, where `varepsilon` is a small constant, the change in the energy of the ground state, to first order in `epsilon`, is
  1. `(5epsilon)/pi`
  2. `(10epsilon)/(3pi)`
  3. `(8epsilon)/(3pi)` ✅
  4. `(4epsilon)/pi`

Q6

For the given logic circuit, the input waveforms A, B, C and D are shown as a function of time

To obtain the output Y as shown in the figure, the logic gate X should be 
  1. an AND gate 
  2. an OR gate  ✅
  3. a NAND gate
  4. a NOR gate

Q7

A small circular wire loop of radius a and number of turns N, is oriented with its axis parallel to the direction of the local magnetic field B. A resistance R and a galvanometer are connected to the coil, as shown in the figure
When the coil is flipped (i.e., the direction of its axis is reversed) the galvanometer measures the total charge Q that flows through it. If the induced emf through the coil `E_F=IR` , then Q is
  1. `(piNa^2B)/(2R)`
  2. `(piNa^2B)/R`
  3. `(sqrt2piNa^2B)/R`
  4. `(2piNa^2B)/R` ✅

Q8

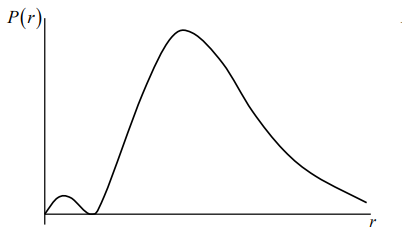
The radial wavefunction of hydrogen atom with the principal quantum number `n=2` and the orbital quantum number `l=0` is `R_20=N(1-r/(2a))e^(-r/(2a))`, where N is the normalization constant. The best schematic representation of the probability density`P(r)` for the electron to be between r and r+dr is
  1.  ✅ 
     




Q9

The matrix `M=((3,-1,2),(-1,2,0),(2,0,1))` satisfies the equation `M^3+alphaM^2+betaM+3=0` if `(alpha,beta)` are 
  1. (-2,2)
  2. (-3,3)
  3. (-6,6) ✅
  4. (-4,4)

Q10

The value of the integral `I=int_0^ooe^(-x)xsin(x)dx` is
  1. 3/4
  2. 2/3
  3. 1/2 ✅
  4. 1/4

Q11

A long cylindrical wire of radius R and conductivity `sigma` , lying along the z -axis, carries a uniform axial current density I . The Poynting vector on the surface of the wire is (in the following `hatrho` and `hatphi` denote the unit vectors along the radial and azimuthal directions respectively)
  1. `(I^2R)/(2sigma)hatrho`
  2. `-(I^2R)/(2sigma)hatrho` ✅
  3. `-(I^2piR)/(4sigma)hatphi`
  4. `(I^2piR)/(4sigma)hatphi`

Q12

A  one-dimensional rigid rod is constrained to move inside a sphere such that its two ends are always in contact with the surface. The number of constraints on the Cartesian coordinates of the endpoints of the rod is
  1. 3 ✅
  2. 5
  3. 2
  4. 4

Q13

Two energy levels, 0 (non-degenerate) and `epsi` (double degenerate), are available to N non-interacting distinguishable particles. If U is the total energy of the system, for large values of N the entropy of the system is `k_B[NlnN-(N-U/epsi)ln(N-U/epsi)+X]` . In this expression, X is 
  1. `-U/epsiln(U/(2epsi))` ✅
  2. `-U/epsiln((2U)/epsi)`
  3. `-(2U)/epsiln((2U)/epsi)`
  4. `-U/epsiln(U/epsi)`

Q14

The minor axis of Earth's elliptical orbit divides the area within it into halves. The eccentricity of the orbit is 0.0167. The difference in time spent by Earth in the two halves is closest to 
  1. 3.9 days  ✅
  2. 4.8 days 
  3. 12.3 days 
  4. 0 days

Q15

In the circuit below, there is a voltage drop of 0.7 V across the diode D in forward bias, while no current flows through it in reverse bias.
If `V_in` is a sinusoidal signal of frequency 50 Hz with an RMS value of 1 V, the maximum current that flows through the diode is closest to 
  1. 1 A 
  2. 0.14 A 
  3. 0 A  ✅
  4. 0.07 A 

Q16

The dispersion relation of a gas of non-interacting bosons in two dimensions is `E(k)=csqrt|k|` , where c is a positive constant. At low temperatures, the leading dependence of the specific heat on temperature T , is
  1. `T^4` ✅
  2. `T^3`
  3. `T^2`
  4. `T^(3/2)`

Q17

The locus of the curve `Im((pi(x-1)-1)/(z-1))=1` in the complex z -plane is a circle centred at `(x_0,y_0)` and radius R . The values of `(x_0,y_0)` and R , respectively, are 
  1. (1,1/2) and 1/2 ✅
  2. (1,-1/2) and 1/2
  3. (1,1) and 1
  4. (1,-1) and 1

Q18

The energy levels available to each electron in a system of N non-interacting electrons are `E_n=nE_0, n=0,1,2,...` . A magnetic field, which does not affect the energy spectrum, but completely polarizes the electron spins, is applied to the system. The change in the ground state energy of the system is
  1. `1/2N^2E_0`
  2. `N^2E_0`
  3. `1/8N^2E_0`
  4. `1/4N^2E_0` ✅

Q19

The value of `<<L_x^2>>` in the state `|phi>>` for which `L^2|phi>>`=`6cancel(h)^2|phi>>` and `L_z|phi>>=2cancel(h)|phi>>` is
  1. 0
  2. `4cancel(h)^2`
  3. `2cancel(h)^2`
  4. `cancel(h)^2` ✅

Q20

A charged particle moves uniformly on the xy -plane along a circle of radius a centred at the origin. A detector is put at a distance d on the x -axis to detect the electromagnetic wave radiated by the particle along the x -direction. If, the wave received by the detector is 
  1. Unpolarised 
  2. Circularly polarized with the plane of polarization being the yz -plane  ✅
  3. Linearly polarized along the y -direction 
  4. Linearly polarized along the z -direction

Q21

The single particle energies of a system of N non-interacting fermions of spin s (at T=0 ) are `E_n=n^2E_0,n=1,2,3,...`. The ratio `(epsi_F(3/2))/(epsi_F(1/2))` of the Fermi energies for fermions of spin 3/2 and spin 1/2, is
  1. 1/2
  2. 1/4 ✅
  3. 2
  4. 1

Q22

The Hamiltonian of a two particle system is `H=p_1p_2+q_1q_2` , where `q_1`and `q_2` are generalized coordinates and `p_1` and `p_2` are the respective canonical momenta. The Lagrangian of this system is
  1. `dotq_1dotq_2+q_1q_2` 
  2. `-dotq_1dotq_2+q_1q_2`
  3. `-dotq_1dotq_2-q_1q_2`
  4. `dotq_1dotq_2-q_1q_2` ✅

Q23

The electric potential on the boundary of a spherical cavity of radius R, as a function of the polar angle `theta` , is `V_0cos^2(theta/2)`. The charge density inside the cavity is zero everywhere. The potential at a distance R 2 from the centre of the sphere is
  1. `1/2V_0(1+1/2costheta)` ✅
  2. `1/2V_0costheta`
  3. `1/2V_0(1+sintheta)`
  4. `1/2V_0sintheta`

Q24

A circuit needs to be designed to measure the resistance R of the a cylinder PQ to the best possible accuracy, using an ammeter A, a voltmeter V, a battery E and a current source `I_s` (all assumed to be ideal). The value of R is known to be approximately `10Omega` , and the resistance W of each of the connecting wires is close to `10Omega` . If the current from the current source and voltage from the battery are known exactly, which of the following circuits
  1. (b)
  2. (a) ✅
  3. (d)
  4. (c)

Q25

The trajectory of a particle moving in a plane is expressed in polar coordinates `(r,theta)` by the equations `r=r_0e^(betat)` and `(d theta)/dt=omega` , where the parameters `r_0,beta` and `omega` are positive. Let `v_r` and `a_r` denote the velocity and acceleration, respectively, in the radial direction. For this trajectory 
  1.  `a_r<0` at all times irrespective of the values of the parameters 
  2.  `a_r>0` at all times irrespective of the values of the parameters 
  3.  `(dv_r)/dt>0` and `a_r>0` for all choices of parameters 
  4.  `(dv_r)/dt>0`, however, `a_r=0` for some choices of parameters ✅

Part C (Any 20)

Q1

Two electrons in thermal equilibrium at temperature `T=k_B/beta` can occupy two sites. The energy of the configuration in which they occupy the different sites is `JvecS_1.vecS_2` (where `J>0` is a constant and `vecS` denotes the spin of an electron), while it is U if they are at the same site. If `U=10J` , the probability for the system to be in the first excited state is
  1. `e^(-(3betaJ)/4)/(3e^((betaJ)/4)+e^(-(3betaJ)/4)+2e^(-10betaJ)`
  2. `(3e^(-(betaJ)/4))/(3e^(-(betaJ)/4)+e^((3betaJ)/4)+2e^(-10betaJ)`✅
  3. `e^(-(betaJ)/4)/(2e^(-(betaJ)/4)+3e^((3betaJ)/4)+2e^(-10betaJ)`
  4. `(3e^(-(3betaJ)/4))/(2e^((betaJ)/4)+3e^(-(3betaJ)/4)+2e^(-10betaJ)`

Q2

Two distinguishable non-interacting particles, each of mass m are in a one-dimensional infinite square well in the interval `[0,a]`. If `x_1`and `x_2` are position operators of the two particles, the expectation value `<<x_1x_2>>` in the state in which one particle is in the ground state and the other one is in the first excited state, is
  1. `1/2a^2`
  2. `1/2pi^2a^2`
  3. `1/4a^2`✅
  4. `1/4pi^2a^2`

Q3

The charge density and current of an infinitely long perfectly conducting wire of radius a , which lies along the z -axis, as measured by a static observer are zero and a constant I , respectively. The charge density measured by an observer, who moves at speed `v=betac` parallel to the wire along the direction of the current, is 
  1. `-(Ibeta)/(pia^2csqrt(1-beta^2))`✅
  2. `-(Ibetasqrt(1-beta^2))/(pia^2c)`
  3. `(Ibeta)/(pia^2csqrt(1-beta^2))`
  4. `(Ibetasqrt(1-beta^2))/(pia^2c)`

Q4

Electrons polarized along the x -direction are in a magnetic field `B_1hati+B_2(hatjcos omega t+hatk sin omega t)`, where `B_1,B_2` and `omega` are positive constants. The value of `cancel(h)omega ` for which the polarization-flip process is a resonant one, is
  1. `2mu_B|B_2|`
  2. `mu_B|B_1|`
  3. `mu_B|B_2|`
  4. `2mu_B|B_1|`✅

Q5

The nucleus of `K^40` (of spin-parity `4^+` in the ground state) is unstable and decays to `Ar^40` . The mass difference between these two nuclei is `DeltaMc^2=1504.4`keV . The nucleus `Ar^40` has an excited state at 1460.8 keV with spin-parity `2^+` . The most probable decay mode of `K^40` is by
  1. a `beta^+` -decay to the `2^+` state of `Ar^40` 
  2. an electron capture to the `2^+` state of `Ar^40`✅
  3. an electron capture to the ground state of `Ar^40` 
  4. a `beta^+` -decay to the ground state of `Ar^40`

Q6

The bisection method is used to find a zero `x_0` of the polynomial `f(x)=x^3-x^2-1` . Since `f(1)=-1` , while `f(2)=3` the values a =1 and b = 2 are chosen as the boundaries of the interval in which the `x_0` lies. If the bisection method is iterated three times, the resulting value of `x_0` is
  1. 15/8
  2. 13/8
  3. 11/8✅
  4. 9/8

Q7

The Hall coefficient `R_H` of a sample can be determined from the measured Hall voltage `V_H=1/dR_HBI+RI` , where d is the thickness of the sample, B is the applied magnetic field, I is the current passing through the sample and R is an unwanted offset resistance. A lock-in detection technique is used by keeping I constant with the applied magnetic field being modulated as `B=B_0sinOmegat` , where `B_0` is the amplitude of the magnetic field and `Omega` is frequency of the reference signal. The measured `V_H` is 
  1. `B_0(R_HI)/d`
  2. `B_0/sqrt2(R_HI)/d`✅
  3. `I/sqrt2((R_HB_0)/d+R)`
  4. `I((R_HB_0)/d+R)`

Q8

The electric and magnetic fields at a point due to two independent sources are `vecE_1=E(alphahati+betahatj)`, `B_1=Bhatk` and `hatE_2=Ehati,hatB_2=-2Bhatk` where `alpha,beta,E` and `B` are constants. If the Poynting vector is along `hati+hatj` , then
  1. `alpha+beta+1=0`✅
  2. `alpha+beta-1=0`
  3. `alpha+beta+2=0`
  4. `alpha+beta-2=0`

Q9

For the transformation `x->X=(alphap)/x,p->P=betax^2` between conjugate pairs of a coordinate and its momentum, to be canonical, the constants `alpha` and `beta` must satisfy
  1. `1+1/2alphabeta=0`
  2. `1-1/2alphabeta=0`
  3. `1+2alphabeta=0`✅
  4. `1-2alphabeta=0`

Q10

A random variable Y obeys a normal distribution `P(Y)=1/(sigmasqrt(2pi))exp[-(Y-mu)^2/(2sigma^2)]`. The mean value of `e^Y` is
  1. `e^(mu+sigma^2/2)`✅
  2. `e^(mu-sigma^2)`
  3. `e^(mu+sigma^2)`
  4. `e^(mu-sigma^2/2)`

Q11

Two operators A and B satisfy the commutation relations `[H,A]=-cancel(h)omegaB` and `[H,B]=-cancel(h)omegaA` , where `omega` constant and H is the Hamiltonian of the system. The expectation value `<<A>>_psi(t)=<<psi|A|psi>>` in a state `|psi>>` , such that at time `t=0,<<A>>_psi(0)=0` and `<<B>>_psi(0)=i` , is
  1. `sin(omegat)`
  2. `sinh(omegat)`✅
  3. `cos(omegat)`
  4. `cosh(omegat)`

Q12

An infinitely long solenoid of radius `r_0` centred at origin which produces a time-dependent magnetic field `alpha/(pir_0^2)cosomegat` (where alpha and omega are constants) is placed along the z -axis. A circular loop of radius R , which carries unit line charge density is placed, initially at rest, on the xy -plane with its centre on the z -axis. If `R>r_0` , the magnitude of the angular momentum of the loop is
  1. `alpha R(1-cosomegat)`✅
  2. `alphaRsinomegat`
  3. `1/2alphaR(1-cos2omegat)`
  4. `1/2alphaRsin2omegat`

Q13

The energy (in keV) and spin-parity values `E(J^p)` of the low lying excited states of a nucleus of mass number A=152 are `122(2^+),366(4^+),707(6^+)` and `1125(8^+)` . It may be inferred that these energy levels correspond to a 
  1. Rotational spectrum of a deformed nucleus✅
  2. Rotational spectrum of a spherically symmetric nucleus 
  3. Vibrational spectrum of a deformed nucleus 
  4. Vibrational spectrum of a spherically symmetric nucleus

Q14

A layer of ice has formed on a very deep lake. The temperature of water, as well as that of ice at the ice-water interface, are 0°C, whereas the temperature of the air above is -10°C. The thickness L(t) of the ice increases with time t . Assuming that all physical properties of air and ice are independent of temperature, `L(t)~L_0t^alpha` for large t . The value of `alpha` is
  1. 1/4
  2. 1/3
  3. 1/2✅
  4. 1

Q15

The electron cloud (of the outermost electrons) of an ensemble of atoms of atomic number Z is described by a continuous charge density `rho(r)` that adjusts itself so that the electrons at the Fermi level has zero energy. If `V(r)` is the local electrostatic potential, then `rho(r)` is
  1. `e/(3pi^2 cancel(h)^3)[2m_eeV(r)]^(3/2)`✅
  2. `(Ze)/(3pi^2 cancel(h)^3)[2m_eeV(r)]^(3/2)`
  3. `e/(3pi^2 cancel(h)^3)[Zm_eeV(r)]^(3/2)`
  4. `e/(3pi^2 cancel(h)^3)[m_eeV(r)]^(3/2)`

Q16

In the circuit shown below, four silicon diodes and four capacitors are connected to a sinusoidal voltage source of amplitude in `V_"in">0.7V` and frequency 1 kHz. If the knee voltage for each of the diodes is 0.7 V and the resistances of the capacitors are negligible, the DC output voltage `V_"out"` after 2 seconds of starting the voltage source is closest to
  1. `4V_"in"-0.7V`
  2. `4V_"in"-2.8V`✅
  3. `V_"in"-0.7V`
  4. `V_"in"-2.8V`

Q17

The dispersion relation of electrons in three dimensions is `epsi(k)=cancel(h)nu_Fk` , where `nu_F` is the Fermi velocity. If at low temperatures `T<T_F` the Fermi energy `epsi_F` depends on the number density n as `epsi_F(n)~n^alpha` , the value of `alpha` is
  1. 1/3✅
  2. 2/3
  3. 1
  4. 3/5

Q18

A system of two identical masses connected by identical springs, as shown in the figure, oscillates along the vertical direction.
The ratio of the frequencies of the normal modes is
  1. `sqrt(3-sqrt5):sqrt(3+sqrt5)`✅
  2. `(3-sqrt5) :(3+sqrt5)`
  3. `sqrt(5-sqrt3) :sqrt(5+sqrt3)`
  4. `(5-sqrt3) :(5+sqrt3)`

Q19

Two random walkers A and B walk on a one-dimensional lattice. The length of each step taken by A is one, while the same for B is two, however, both move towards right or left with equal probability. If they start at the same point, the probability that they meet after 4 steps, is
  1. 9/64
  2. 5/32
  3. 11/64✅
  4. 3/16

Q20

The phase shifts of the partial waves in an elastic scattering at energy E are `delta_0=12^circ,delta_1=4^circ` and `delta_(l>=2)=0^circ` . The best qualitative depiction of `theta`-dependence of the differential scattering cross-section `(dsigma)/(dcostheta)` is 

Q21

The matrix `R_(hatn)(theta)` represents a rotation by an angle `theta` about the axis `hatn` . The value of `theta` and `hatn` corresponding to the matrix `((-1,0,0),(0,-1/3,(2sqrt2)/3),(0,(2sqrt2)/3,1/3))` , respectively, are
  1. `pi/2" and "(0,-sqrt(2/3),1/sqrt3)`
  2. `pi/2" and "(0,1/sqrt3,sqrt(2/3))`
  3. `pi" and "(0,-sqrt(2/3),1/sqrt3)`
  4. `pi" and "(0,1/sqrt3,sqrt(2/3))`✅

Q22

In a one-dimensional system of N spins, the allowed values of each spin are `sigma_i={1,2,3,...,q}` , where `q >= 2` is an integer. The energy of the system is `-Jsum_(i=1)^Ndelta_(sigma_i,sigma_(i+1))` where `J>0` is a constant. If periodic boundary conditions are imposed, the number of ground states of the system is
  1. `q`✅
  2. `Nq`
  3. `q^N`
  4. 1

Q23

The red line of wavelength 644 nm in the emission spectrum of Cd corresponds to a transition from the `D_2^1` level to the `P_1^1` level. In the presence of a weak magnetic field, this spectral line will split into (ignore hyperfine structure) 
  1. 9 lines 
  2. 6 lines 
  3. 3 lines ✅
  4. 2 lines

Q24

Let the separation of the frequencies of the first Stokes and the first anti-Stokes lines in the pure rotational Raman Spectrum of the `H_2` molecule be `Deltanu(H_2)` , while the corresponding quantity for `D_2` is `Deltanu(D_2)` . The ratio `(Deltanu(H_2))/(Deltanu(D_2))` is
  1. 0.6
  2. 1.2
  3. 1
  4. 2✅

Q25

The value of the integral `int_-oo^oodxe^(-|x|/pi)delta(sinx)` where `delta(x)` is the Dirac delta function, is
  1. 3✅
  2. 0
  3. 5
  4. 1

Q26

A neutral particle `X^0` is produced in `pi^(-)+P->X^0+n` by s-wave scattering. The branching ratio of the decay of `X^0` to `2gama,3pi` and `2pi` are 0.38, 0.30 and less than `10^-3` , respectively. The quantum numbers `J^"CP"` of `X^0` are
  1. `0^"-+"`
  2. `0^(+ -)`✅
  3. `1^"-+"`
  4. `1^(+ -)`

Q27

If the Bessel function of integer order n is defined as `J_n(x)=sum_(k=0)^oo(-1)^k/(k!(n+k)!)(x/2)^(2k+n)` then `d/dx[x^-nJ_n(x)]` is 
  1. `-x^(-(n+1))J_(n+1)(x)`
  2. `-x^(-(n+1))J_(n-1)(x)`
  3. `-x^(-n)J_(n-1)(x)`
  4. `-x^(-n)J_(n+1)(x)`✅

Q28

A train of impulses of frequency 500 Hz, in which the temporal width of each spike is negligible compared to its period, is used to sample a sinusoidal input signal of frequency 100 Hz. The sampled output is 
  1. Discrete with the spacing between the peaks being the same as the time period of the sampling signal ✅
  2. A sinusoidal wave with the same time period as the sampling signal 
  3. Discrete with the spacing between the peaks being the same as the time period of the input signal 
  4. A sinusoidal wave with the same time period as the input signal

Q29

The angular width `theta` of a distant star can be measured by the Michelson radiofrequency stellar interferometer (as shown in the figure below). 
The distance h between the reflectors `M_1` and `M_2` (assumed to be much larger than the aperture of the lens), is increased till the interference fringes (at `P_0,P` on the plane as shown) vanish for the first time. This happens for h=3 m for a star which emits radiowaves of wavelength 2.7 cm. The measured value of `theta` (in degrees) is closest to
  1. 0.63✅
  2. 0.32
  3. 0.52
  4. 0.26

Q30

A lattice A consists of all points in three-dimensional space with coordinates `(n_x,n_y,n_z)` where , `n_x,n_y` and `n_z` are integers with `n_x+n_y+n_z` being odd integers. In another lattice B, `n_x+n_y+n_z` are even integers. The lattices A and B are 
  1. both BCC 
  2. both FCC ✅
  3. BCC and FCC, respectively 
  4. FCC and BCC, respectively




Next Post Previous Post
No Comment
Add Comment
comment url