CSIR NET Physics Dec 2023 Year Question & Answer

Physics INK
9 Jan, 2024

 CSIR NET Physics Dec 2023

Part A : Marks-2

Question 1:

SCRIPT : DIRECTOR :: ??: CHEF 
Choose the most appropriate option from the following to fill the blank
  1. MENU 
  2. RECIPE 
  3. RESTAURANT
  4. MEAL 
Answer: 2

Question 2:

The time seen in a mirror placed opposite a numberless analog (with hands) wall clock is 4h 55 min. What approximately is the correct time? 
  1. 4h55 min
  2. 5h05 min 
  3. 7h05 min 
  4. 1h35 min 
Answer: 3

Question 3:

The sum of the two positive integers is 14. Then their product CANNOT be divisible by
  1. 12
  2. 13
  3. 14
  4. 49 
Answer: 3

Question 4: 

A person’s viral load measured in some unit was 15, 25, 50, 200, 300, 150 and 30 on days 1 to 7. respectively. The maximum relative change took place between 
  1.  day 3 to day 4. 
  2.  day 4 to day 5. 
  3.  day 5 to day 6. 
  4.  day 6 to day 7, 
Answer: 1

Question 5:

A truck from a post office is sent to collect post from a plane as per schedule. The plane lands ahead of schedule, therefore its contents are transported by a rickshaw. The rickshaw meets the truck 30 minutes after the arrival of plane, and the post is transferred. The truck returns to the post office 20 minutes early. How early did the plane arrive? (Assume all transactions are instantaneous.) 
  1. 10 minutes 
  2. 20 minutes
  3. 30 minutes 
  4. 40 minutes 
Answer: 4

Question 6:

A bird keeps flying continuously between two trains, that are following each other on a straight track. The train behind is slower than the one ahead by 1.5 kmv/h. If the speed of the bird is 20 km/h, what distance would the bird cover in an hour? 
  1. 20km 
  2. 30km 
  3. 50km
  4. 60km 
Answer: 1

Question 7:

A letter is drawn at random from the following string of letters. 
RAMUKYAJNAS 
What is the probability that it is NOT a vowel? 
  1. 1/2
  2. 6/11
  3. 711
  4. 8/11
Answer: 3

Question 8:

All the four entries in column A must be matched with all those in column B. Each correctly matched option gets one mark and no mark is awarded otherwise. Which of the following mark(s) CANNOT be scored?
  1. 3
  2. 1
  3. 2
  4. 4
Answer: 1

Question 9:

In 1979, Ramesh’s age was the sum of the digits of his year of birth. In 2017, on his birthday. what was his age?
  1. 49
  2. 57
  3. 60
  4. 64
Answer: 3

Question 10:

For every 5 chocolates that Ramesh gets, Suresh gets 3 chocolates. Geeta gets 3 chocolates for every 2 chocolates that Suresh gets. If Geeta has 18 chocolates. then the sum of chocolates with Ramesh and Suresh is
  1. 16
  2. 30
  3. 32
  4. 38
Answer: 3

Question 11:

Radius of a sphere is measured with 5% uncertainty, What is the uncertainty in the volume. determined from this radius?
  1. 5% 
  2. 6.6% 
  3. 125% 
  4. 15% 
Answer: 4

Question 12:

In how many ways can a menu be made from 5 dishes, if the menu contains either 3 or 4 dishes? 
  1. 2
  2. 3
  3. 7
  4. 15
Answer: 4

Question 13:

If `a <x < b`, then for which of the following relations does `0 < y < 1` always hold? 
  1. `y=(a-x)/(b+a)`
  2. `y=(x-a)/(b-a)`
  3. `y=(x-b)/(b-a)`
  4. `y=(b-x)/(a+b)`
Answer: 2

Question 14:

What is the value of x in the given magic square. (i.e. a square grid in which the sum of the numbers in rows. columns and diagonals is the same)?
 
  1. 6
  2. 4
  3. 3
  4. 1
Answer: 1

Question 15:

In the figure `log_(10)y` is plotted against `log_(10)x`
When y is plotted against x. then the plot in the provided range is 
  1. A
  2. B
  3. C
  4. D
Answer: 4

Question 16

What is the minimum number of pourings needed to get 4 litre of milk from a fully filled 8 litre can, using ungraduated empty 5 and 3 litre cans? No milk should be wasted.
  1. 4
  2. 5
  3. 6
  4. 8
Answer: 3

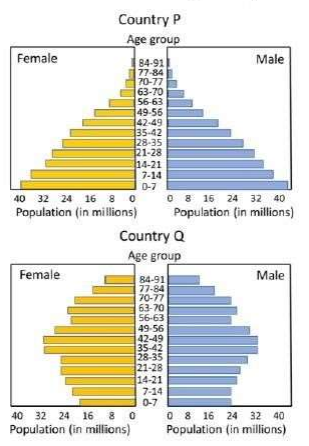
Question 17

The figure shows age-wise bar graph of male and female population of two countries. Which one of the following is likely to be true?
  
  1. Country Q has higher life expectancy
  2. Country P has higher per-capita income
  3. The population of country P is decreasing more rapidly than Q
  4. Country P has better health facilities 
Answer: 1 

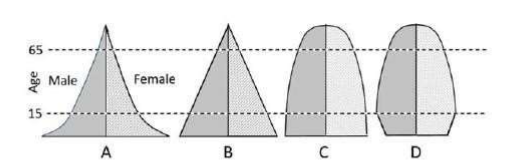
Question 18

The above figures show population pyramids to four countries A, B. C and D. The country showing the most stable population is
  1. C
  2. A
  3. B
  4. D
Answer: 1

Question 19

In a market. you can buy a mango for Rs.10. a lemon for Re 1 and 8 chillies for Re 1. How many of these items do you need to buy to get a mix of 100 items for exactly Rs. 100? 
  1. 6 mangoes, 22 lemons, 72 chillis 
  2. 7 mangoes, 21 lemons. 72 chillis
  3. 1 mango, 9 lemons, 80 chillis
  4. 8 mangoes, 12 lemons. 80 chillis
Answer: 2

Question 20

Four children had 27 apples among them. No child had less than 5 apples. If no two children had the same number of apples. then which of the following could NOT be the number of apples a child had?
  1. 5
  2. 6
  3. 8
  4. 9
Answer: 3

 Part B : Marks- 3.5

Question 1:

A particle of unit mass subjected to the 1-dimensional potential `V(x)=(2alpha)/x^3-(3beta)/x^2` executes small oscillations about its equilibrium position, where `alpha` and `beta`positive constants with appropriate dimensions. The time period of small oscillations is 
  1. `(pi alpha^2)/sqrt(6beta^5)`
  2. `(pi alpha^2)/sqrt(3beta^5)`
  3. `(2pi alpha^2)/sqrt(3beta^5)`
  4. `(2pi alpha^2)/sqrt(6beta^5)`
Answer: 4

Question 2:

A particle of mass `m` is moving in a stable circular orbit of radius `r_0` with angular momentum `L`. For a potential energy `V(r) = beta r^k` (`beta > 0` and `k > 0`), which of the following options is correct? 
  1. `k=2,r_0=((3L^2)/(5mbeta))^(1/5)`
  2. `k=2,r_0=((L^2)/(2mbeta))^(1/4)`
  3. `k=2,r_0=((L^2)/(4mbeta))^(1/4)`
  4. `k=3,r_0=((5L^2)/(3mbeta))^(1/5)`
Answer: 2

Question 3:

For three inputs A, B and C, the minimum number of 2-input NAND gates required to generate the output `Y= bar(A+B)+barC` is  
  1. 3
  2. 4
  3. 7
  4. 6
Answer: 2

Questions 4:

The branch line for the function `f(z)=sqrt((z^2-5z+6)/(z^2+2z+1))` is
Answer: 3

Question 5:

The coordinates of the following events in an observer's inertial frame of reference are as follows: 
Event 1: `t_1 = 0, x_1 = 0` :A rocket with uniform velocity `0.5c` crosses the observer at origin along x axis 
Event 2: `t_2 =T, x_2 = 0` : The observer sends a light pulse towards the rocket 
Event 3: `t_3,x_3` : The rocket receives the light pulse 
The values of `t_3, x_3` respectively are  
  1. `2T,cT`
  2. `2T,c/2T`
  3. `sqrt3 /2T, 2/sqrt3 cT`
  4. `2/sqrt3T,sqrt3/2cT`
Answer: 1

Question 6

The light incident on a solar ceil has a uniform photon flux in the energy range of 1 eV to 2 eV and is zero elsewhere. The active layer of the cell has a bandgap of 1.5eV and absorbs 80% of the photons with energies above the bandgap. Ignoring non-radiative losses, the power conversion efficiency (ratio of the output power to the input power) is closest to 
  1. 47%
  2. 70%
  3. 23%
  4. 35%
Answer: 1

Question 7

The Hamiltonian for two particles with angular momentum quantum numbers `l_1=l_2=1`, is
`hatH=e/cancelh^2[(hatL_1+hatL_2).hatL_2-(hatL_(1z)+hatL_(2z))^2]`
lf the operator for the total angular momentum is given by `hatL=hatL_1+hatL_2`, then the possible energy eigenvalues for states with `l=2`, (where the eigenvalues of `hat(L^2)` are `l(l+1)cancelh^2` ) are
  1. `3epsi,2epsi,-epsi`
  2. `6epsi,5epsi,2epsi`
  3. `3epsi,2epsi,epsi`
  4. `-3epsi,-2epsi,epsi`
Answer: 1

Question 8

In the circuit shown below using an ideal opamp, inputs `V_j(j = 1,2,3,4)` may either be open or connected to a -5 V battery. 
The minimum measurement range of a voltmeter to measure all possible values of `V_"out"` is 
  1. 10V
  2. 30V
  3. 3V
  4. 1V
Answer: 1

Question 9

If z is a complex number, which among the following sets is neither open nor closed?
  1. `{z|0<=|z-1|<=2}`
  2. `{z||z|<=2}`
  3. `{z|zin(CC-{3})"and " |z|<=100}`
  4. `{z|z=re^(itheta),0<=theta<=pi/4}` 
Answer: 3

Question 10

Each allowed energy level of a system of non-interacting fermions has a degeneracy M. If there are N fermions and R is the remainder upon dividing N by M, then the degeneracy of the ground state is 
  1. `R^M`
  2. `1`
  3. `M`
  4. `""^MC_R`
Answer: 4

Question 11

Let M be a `3xx3` real matrix such that 
`e^(Mtheta)=[[cos theta, sintheta,0],[-sintheta, cos theta,0],[0,0,1]]` 
where `theta` is a real parameter. Then M is given by
  1. `[[-1,0,0],[0,1,0],[0,0,0]]`
  2. `[[0,1,0],[-1,0,0],[0,0,0]]`
  3. `[[0,0,1],[0,-1,0],[0,0,0]]`
  4. `[[1,0,0],[0,-1,0],[0,0,1]]`
Answer: 2

Question 12

The normalized wave function of an electron is 
`psi(vecr)=R(r)[sqrt(3/8)Y_1^0(theta,phi)chi_"-"+sqrt(5/8)Y_1^1(theta,phi)chi_+]` 
where `Y_l^m` are the normalized spherical harmonics and `chi_+-` denote the wavefunction for the two spin states with eigenvalues `+-cancelh`. The expectation value of the z component of the total angular momentum in the above state is 
  1. `-3/4cancelh`
  2. `3/4cancelh`
  3. `-9/8cancelh`
  4. `9/8cancelh`
Answer: 2

Question 13

A system of N non-interacting classical spins, where each spin can take values `sigma=-1,0,1` , is placed in a magnetic field `h`. The single spin Hamiltonian is given by 
`H=-mu_Bhsigma+Delta(1-sigma^2)`, 
 where`mu_B,Delta` are positive constants with appropriate dimensions. If `M` is the magnetization, the zero-field magnetic susceptibility per spin `1/N(delM)/(delh)|_(h->0)` at atemperature T = 1/`betak_B`, is given by  

  1. `betamu_B^2`
  2. `(2betamu_B^2)/(2+e^(-betaDelta))`
  3. `betamu_B^2e^(-betaDelta)`
  4. `(betamu_B^2)/(1-e^(-betaDelta)`
Answer: 2

Question 14

A particle moves in a circular orbit under a force field given by `vecF(vecr)=-k/r^2hatr` where k is a positive constant. If the force changes suddenly to `vecF(vecr)=-k/(2r^2)hatr`, the shape of the new orbit would be
  1. parabolic
  2. circular
  3. elliptical
  4. hyperbolic 
Answer: 1

Question 15

The Schrdédinger wave function for a stationary state of an atom in spherical polar coordinates `(r,theta,phi)` is
`psi=af(r)costheta sintheta e^(iphi)`
where A is the normalization constant. The eigenvalue of `hatL_z`, for this state is  
  1. `2cancelh`
  2. `cancelh`
  3. `-2cancelh`
  4. `-cancelh`
Answer: 2

Question 16

For a flat circular glass plate of thickness `d`, the refractive index `n(r)` varies radially, where `r` is the radial distance from the centre of the plate. A coherent plane wavefront is normally incident on this plate as shown in the figure below.


 If the emergent wavefront is spherical and centered on the axis of the plate, then `n(r) - n(0)` should be proportional to
  1. `r^(1/2)`
  2. `r`
  3. `r^2`
  4. `r^(3/2)`
Answer: 3

Question 17

The 1-dimensional Hamiltonian of a classical particle of mass `m` is 
`H=p^2/(2m)e^(-x/a)+V(x)`
where `a` is a constant with appropriate dimensions. The corresponding Lagrangian is,  
  1. `m/2((dx)/(dt))^2e^(x/a)-V(x)`
  2. `m/2((dx)/(dt))^2e^(-x/a)-V(x)`
  3. `(3m)/2((dx)/(dt))^2e^(x/a)-V(x)`
  4. `(3m)/2((dx)/(dt))^2e^(-x/a)-V(x)`
Answer: 1

Question 18

Aclassical ideal gas is subjected to a reversible process in which its molar specific heat changes with temperature T as `C(T)=C_V+RT/T_0` . If the initial temperature and  volume are `T_0` respectively, and `V_0` the final volume is `2V_0` then the final temperature is 
  1. `T_0/ln2`
  2. `2T_0`
  3. `T_0/[1-ln2]`
  4. `T_0[1+ln2]`
Answer: 4

Question 19

In the measurement of a radioactive sample, the measured counts with and without the sample for equal time intervals are `C=500` and `B= 100`, respectively. The errors in the measurements of C and B are `|DeltaC|=20` and `|DeltaB|=10`, respectively. The net error `|DeltaY|` in the measured counts from the sample `Y=C-B`, is closest to 
  1. 22
  2. 10
  3. 30
  4. 43
Answer: 1

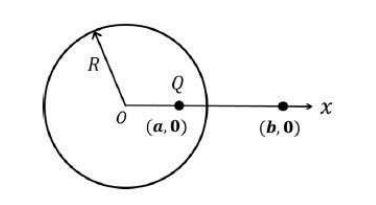
Question 20

A conducting shell of radius R is placed with its centre at the origin as shown below. A point charge Q is placed inside the shell at a distance a along the x-axis from the centre.
The electric field at a distance b > R along the x-axis from the centre is
  1. `Q/(4piepsi_0b^2)hatx`  
  2. `Q/(4piepsi_0)[1/(b-a)^2-(aR)/(ab-R^2)^2]hatx`
  3. `Q/(4piepsi_0)[1/(b-a)^2+(aR)/(ab-R^2)^2]hatx`
  4. `Q/(4piepsi_0)[1/b^2-R^2/(a^2b^2)]hatx`
Answer: 1

Question 21

he Beta function is defined as `B(x,y) =int_0^1t^(x-1)(1-t)^(y-1) dt`. Then `B(x,y + 1)+ B(x + 1, y)` can be expressed as 
  1. B(x,y-1)
  2. B(x+y,1)
  3. B(x+y,x-y)
  4. B(x,y)
Answer: 4

Question 22

A small bar magnet is placed in a magnetic field `B(vecr)=B(x)hatz`. The magnet is initially at rest with its magnetic moment along `haty`. At later times, it will undergo
  1. angular motion in the yz plane and translational motion along `haty`
  2. angular motion in the yz plane and translational motion along `hatx` 
  3. angular motion in the zx plane and translational motion along `hatz` 
  4. angular motion in the xy plane and translational motion along `hatz`  
Answer: 2

Question 23

Aone dimensional infinite long wire with uniform linear charge density `lambda`, is placed along the z-axis. The potential difference `deltaV=V(rho+a)-V(rho)`, between two points at radial distances `rho +a` and `rho` from the z-axis, where `a"<<"rho`, is closest to  
  1. `-lambda/(2piepsi_0)a^2/rho^2`
  2. `-lambda/(2piepsi_0)a/rho`
  3. `lambda/(2piepsi_0)a/rho`
  4. `lambda/(2piepsi_0)a^2/rho^2`
Answer: 2

Question 24

A quantum system is described by the Hamiltonian 
`H=JS_z+lambdaS_x`
where `S_i=h/2sigma_i` and `sigma_i(i=x,y,z)` are the Pauli matrices. If `0<lambda"<<"J`, then the 
leading correction in `lambda` to the partition function of the system at temperature T is 
  1. `(cancelhlambda^2)/(2Jk_BT)coth((Jcancelh)/(2k_BT))`
  2. `(cancelhlambda^2)/(2Jk_BT)tanh((Jcancelh)/(2k_BT))`
  3. `(cancelhlambda^2)/(2Jk_BT)cosh((Jcancelh)/(2k_BT))`
  4. `(cancelhlambda^2)/(2Jk_BT)sinh((Jcancelh)/(2k_BT))`
Answer: 4

Question 25

 Four distinguishable particles fill up energy levels `0,epsi,2epsi`. The number of available microstates for the total energy `4epsi` is
  1. 20
  2. 24
  3. 11
  4. 19
Answer: 4

Part C: Marks -5

Question 1:

Given the data points 
using Lagrange’s method of interpolation, the value of y at x = 4 is closest to 
  1.  54 
  2.  55 
  3.  53 
  4.  56 
Answer: 2

Question 2

A photon inside the sun executes a random walk process. Given the radius of the sun `~~7xx10^8`km  and mean free path of a photon `~~10^-3` m, the time taken by the photon to travel from the centre to the surface of the sun is closest to 
  1. `10^6` sec
  2. `10^24`sec
  3. `10^12` sec
  4. `10^18` sec
Answer: 3

Question 3

The ionization potential of hydrogen atom is 13.6eV, and `lambda_H` and `lambda_D` denote longest wavelengths in Balmer spectrum of hydrogen and deuterium atoms, respectively. Ignoring the fine and hyperfine structures, the percentage difference `y=(lambda_H-lambda_D)/lambda_Hxx100`, is closest to 
  1. 1.0003%
  2. -0.03%
  3. 0.03%
  4. -1.0003%
Answer: 3

Question 4

In a shell model description, neglecting Coulomb effects, which of the following statements for the energy and spin-parity is correct for the first excited state of A = 12 isobars `B_5^12, C_6^12" and " N_7^12`
  1. same for `B_5^12, C_6^12" and " N_7^12`
  2. different for each `B_5^12, C_6^12" and " N_7^12`
  3. same for `C_6^12" and " N_7^12`. but different for `B_5^12,`.
  4. samefor `B_5^12" and "N_7^12`, but different for `C_6^12`
Answer: 4

Question 5

The collision time of the electrons in a metal in the Drude model is `tau` and their plasma frequency is `omega_p`. If this metal is placed between the plates of a capacitor, the time constant associated with the decay of the electric field inside the metal is 
  1. `tau+1/omega_p`
  2. `omega_ptau^2`
  3. `1/(omega_p^2tau)`
  4. `tau/(1+omega_ptau)`
Answer: 3

Question 6

n a quantum harmonic oscillator problem, `hata` and `hat N` are the annihilation operator and the number operator, respectively. The operator `e^(hatN)hatae^(-hatN)` is
  1. `hata`
  2. `e^(-1)hata`
  3. `e^(hatI+hata)`
  4. `e^(hata)`
(Where `hatI` is the identity operator)

Answer: 2

Question 7

In the section of an infinite lattice shown in the figure below, all sites are occupied by identical hard circular discs so that the resulting structure is tightly packed.
The packing fraction is
  1. `(3pi)/4`
  2. `pi/4`
  3. `(3pi)/16`
  4. `(9pi)/16`
Answer: 3

Question 8

A Lagrangian is given by
`L=1/2m(dotx^2+dotydotz+dotz^2)-alpha(2x+3y+z)`
 The conserved momentum is
  1. `m[2dotx+dotz]`
  2. `m[2dotx+doty+dotz]`
  3. `m[dotx+3/2doty+1/2dotz]`
  4. `m[2dotx+3dotz]`
Answer: 2

Question 9

A quantum particle of mass m is moving in a one dimensional potential
`V(x)=V_0theta(x)-lambdadelta(x)`, where `V_0` and `lambda` are positive constants, `theta(x)` is the Heaviside step function and `delta(x)` is the Dirac delta function. The leading contribution to the reflection coefficient for the particie incident from the left with energy `E"> >" V_0 >A` and `sqrt(2mE)">>"(V_0cancelh)/lambda` is 
  1. `V_0^2/(4E^2)`
  2. `V_0^2/(8E^2)`
  3. `(mlambda^2)/(2Ecancelh^2)`
  4. `(mlambda^2)/(4Ecancelh^2)`
Answer: 3

Question 10

An infinite waveform `V(t)` varies as  shown in the figure below
The lowest harmonic that vanishes in the Fourier series of `V(t)` is 
  1. 2
  2. 3
  3. 6
  4. None
Answer: 3

Question 11

The permittivity of a medium `epsi(veck,omega)`, where `omega` and `veck` are the frequency and wavevector, respectively, has no imaginary part. For a longitudinal wave, `veck` is parallel to the electric field such that `veckxxvecE=0`, while for a transverse wave `veck.vecE=0`. In the absence of free charges and free currents, the medium can sustain
  1. longitudinal waves with `veck` and `vecomega` when `epsi(veck,omega)>0`
  2. transverse waves with `veck` and `vecomega` when `epsi(veck,omega)<0`
  3. longitudinal waves with `veck` and `vecomega` when `epsi(veck,omega)=0`
  4. both longitudinal and transverse waves `veck` and `vecomega` when `epsi(veck,omega)>0`
Answer: 3

Question 12

A particle of mass m is moving in a 3-dimensional potential 
`phi(r)=-k/r-k^'/(3r^3)" where " k,k^'>0.`
 For the particle with angular momentum `l`, the necessary condition to have a stable circular orbit is  
  1. `kk^'<l^4/(4m^2)`
  2. `kk^'>l^4/(4m^2)`
  3. `kk^'<l^4/(m^2)`
  4. `kk^'>l^4/(m^2)`
Answer: 1

Question 13

The radius of a sphere oscillates as a function of time as `R+a cos omega t`, with `a < R`. It carries a charge `Q` uniformly distributed on its surface at all times. If `P`  is the time averaged radiated power through a sphere of radius `r`, such that `r">>"R+a` and `r">>"c/omega` . then
  1. `Pprop(Q^2omega^4a^2)/c^3`
  2. `Pprop(Q^2omega^2)/c`
  3. `P=0`
  4. `Pprop(Q^2omega^6a^4)/c^5`
 Answer: 3

Question 14

Atmospheric neutrinos are produced from the cascading decays of cosmic pions `(pi^pm)` to stable particles. Ignoring all other neutrino sources, the ratio of muon neutrino `(nu_mu+barnu_mu)` flux to electron neutrino `(nu_e+barnu_e)` flux in atmosphere is expected to be closest to
  1. 2:3
  2. 1:1
  3. 1:2
  4. 2:1
 Answer: 4

Question 15

A canonical transformation from the phase space coordinates `(q,p)` to `(Q,P)` is generated by the function
 `psi(p,Q)=p^2/(2omega)tan2piQ.`
 where `omega` is a positive constant. The function `omega(p, Q)` is related to `F(q,Q)` by the Legendre transform `psi = pq — F`, where `F` is defined by `dF = pdq — PdQ`. If the solution for `(P,Q)` is 
`P(t)=omega/(4pi)t^2,Q(t)=Q_0="constant"`
 where `t` is time, then the solution for `(p,q)` variables can be written as
  1. `p=(omegat)/(2pi) cos (2piQ_0),q=t/(2pi)sin(2piQ_0)`
  2. `p=-(omegat)/(2pi) cos (2piQ_0),q=t/(2pi)sin(2piQ_0)`
  3. `p=(omegat)/(2pi) sin (2piQ_0),q=t/(2pi)cos(2piQ_0)`
  4. `p=-(omegat)/(2pi) sin (2piQ_0),q=t/(2pi)cos(2piQ_0)`
Answer: 1

Question 16

A solar probe mission detects a fractional wavelength shift `((Delta lambda)/lambda)` of the spectral line `lambda = 630` nm within a sunspot to be of the order of `10^(-5)`. Assuming this shift is caused by the normal Zeeman effect (i.e., neglecting other physical effects), the estimated magnetic field (in tesla) within the observed sunspot is closest to 
  1. `3xx10^(-5)`
  2. `300`
  3. `0.3`
  4. `3xx10^5`
Answer: 3

Question 17

A 2-dimensional resonant cavity supports a TM mode built from a function
`psi(x,y,t)=sin(vecK_a.vecr-omegat)+sin(vecK_b.vecr-omegat)+sin(vecK_a.vecr+omegat)+sin(vecK_b.vecr+omegat)`
where `veck_a`, and `veck_b`, lie in the xy-plane and make angles `pi/4` and `(3pi)/4` with the x-axis, respectively. If `0<|veck_a|<|veck_b|, then which of the following closely describes the outline of the cavity? 

Answer: 2

Question 18

A circuit with operational amplifier is shown in the figure below.
The output voltage waveform `V_"out"` will be closest to 
Answer: 1

Question 19

An incident plane wave with wavenumber `k` is scattered by a spherically symmetric soft potential. The scattering occurs only in S- and P- waves. The approximate scattering amplitude at angles `theta=pi/3` and `theta=pi/2` are 
`f(theta=pi/3)cong1/(2k)(5+3i)" and "f(theta=pi/2)cong1/(2k)(1+(3i)/2) `
Then the total scattering cross-section is closest to
  1. `(37pi)/(4k^2)`
  2. `(10pi)/k^2`
  3. `(35pi)/(4k^2)`
  4. `(9pi)/k^2`
Answer: 1

Question 20

A transmission a line has the characteristic impedance of `(50+ 1j)Omega` and is terminated in a load resistance of `(70- 7j )Omega` (where `j^2 =-1`). The magnitude of the reflection coefficient will be closest to
  1. 5/7
  2. 1/2
  3. 1/6
  4. 1/7
Answer: 3

Question 21

The work done on a material to change its magnetization `M` in an external field `H` is `dW = HdM`. Its Gibbs free energy is 
` G(T,H)=-(gammaT+(aH^2)/(2T))`
where `gamma,a>0` are constants. The material is in equilibrium at a temperature `T=T_0` and in an external field `H=H_0` . If the field is decreased to `H_0/2` adiabatically and reversibly, the temperature changes to 
  1. `2T_0`
  2. `T_0/2`
  3. `(a/(2gamma))^(1/4)sqrt(H_0T_0)`
  4. `(a/(gamma))^(1/4)sqrt(H_0T_0)`
Answer: 2

Question 22

The ground state of  `Pb_82^207` nucleus has spin-parity `J^pi=(1/2)^-`. while the first excited state has `J^pi=(5/2)^-` For the transition from the first excited state to the ground state, possible multipolarities of emitted electromagnetic radiation are 
  1. E2,E3
  2. M2,M3
  3. M2,E3
  4. E2,M3
Answer: 4

Question 23

In the rotational-vibrational spectrum of an idealized carbon monoxide (CO) molecule, ignoring rotational-vibrational coupling, two transitions between adjacent vibrational levels with wavelength `lambda_1` and `lambda_2` correspond to the rotational transition from `J^' = 0` to `J^('') =1`,and `J^' = 1` to `J^('') =0`, respectively. Given that the reduced mass of CO is `1.2xx10^(-26)`kg, equilibrium bond length of CO is 0.12 nm and vibrational frequency is `5xx10^13` Hz, the ratio of`lambda_1/lambda_2` is closest to
  1. 0.9963
  2. 0.0963
  3. 1.002
  4. 1.203
Answer: 1

Question 24

The function `f(z)=1/((z+1)(z+3))` is defined on the complex plane. The coefficient of the `(z-z_0)^2` term of the Laurent series of `f(z)` about `z_0 = l` is 
  1. 1/64
  2. 7/128
  3. 9/64
  4. 9/128
Answer: 2

Question 25

A system of non-relativistic and non-interacting bosons of mass `m` in two dimensions has a density `n`. The Bose-Einstein condensation temperature `T_c` is 
  1. `(12ncancelh^2)/(pimk_B)`
  2. `(3ncancelh^2)/(pimk_B)`
  3. `(6ncancelh^2)/(pimk_B)`
  4. 0
Answer: 0

Question 26

The solution `y(x)` of the differential equation `y^('')+y/4=x/2` where `0<=x<=pi` ,together with the boundary conditions `y(0) = y(pi) = 0` is  
  1. `2/pisum_(n=1)^oo(-1)^npi/n(sinnx)/(1/4-n^2)`
  2. `2/pisum_(n=1)^oo(-1)^npi/(2n)(sinnx)/(1/4-n^2)`
  3. `2/pisum_(n=1)^oo(-1)^(n+1)pi/n(sinnx)/(1/4-n^2)`
  4. `2/pisum_(n=1)^oo(-1)^(n+1)pi/(2n)(sinnx)/(1/4-n^2)`
Answer: 4

Question 27

A quantum system is described by the Hamiltonian 
 `H=-Jsigma_z+lambda(t)sigma_x`
 where `sigma_i (i = x, y,z)` are Pauli matrices, `J` and `lambda` are positive constants `(J ">>"lambda )`  and 
`lambda(t)={(0,"for",t<0),(lambda,"for ",0<t<T),(0,"for",t>T):}`
At `t < 0`, the system is in the ground state. The probability of finding the system in the excited state at `t ">>"T` , in the leading order in `lambda` is 
  1. `lambda^2/(8J^2)sin^2((JT)/cancelh)`
  2. `lambda^2/(J^2)sin^2((JT)/cancelh)`
  3. `lambda^2/(4J^2)sin^2((JT)/cancelh)`
  4. `lambda^2/(16J^2)sin^2((JT)/cancelh)`
Answer: 2

Question 28

The lattice constant of the bec structure of sodium metal is `4.22 A^@`. Assuming the mass of the electron inside the metal to be the same as free electron mass, the free electron Fermi energy is closest to
  1. 3.2eV
  2. 2.9eV
  3. 3.5eV
  4. 2.5 eV  
Answer: 1

Question 29

Gauge factor of a strain gauge is defined as the ratio of the fractional change in resistance `((DeltaR)/R)` to the fractional change in length `((DeltaL)/L)` A metallic strain gauge with a gauge factor 2 has a resistance of `100 Omega` under unstrained condition. An aluminum foil with Young's modulus `Y = 70 (GN)/m^2` is installed on the metallic gauge. Keeping the foil within its elastic limit, a stress of `0.2(GN)/m^2` is applied on the foil. The change in the resistance of the gauge will be closest to 
  1. `0.14Omega`
  2. `1.23Omega`
  3. `0.28Omega`
  4. `0.56Omega`
Answer: 4

Question 30

The regular representation of two nonidentity elements of the group of order 3 are given by
  1. `((0,1,0),(1,0,0),(0,0,1)),((0,0,1),(0,1,0),(1,0,0))`
  2. `((1,0,0),(0,0,1),(0,1,0)),((0,1,0),(1,0,0),(0,0,1))` 
  3. `((0,0,1),(1,0,0),(0,1,0)),((0,1,0),(0,0,1),(1,0,0))`
  4. `((0,0,1),(0,1,0),(1,0,0)),((0,0,1),(1,0,0),(0,1,0))`
Answer: 3
Previous Post
No Comment
Add Comment
comment url