Magnetic field of a solenoid
Magnetic field of a solenoid
Physics INK
Find the magnetic field at point P on the axis of a tightly wound solenoid (helical coil) consisting of n turns per unit length wrapped around a cylindrical tube of radius a and carrying current I. Express your answer in terms of 8 and 8. Consider the turns to be essentially circular, and use the result. What is the field on the axis of an infinite solenoid (infinite in both directions)?
A solenoid is an infinite number of circular loops carrying current `I`. Let us consider a circular loop with no of turn `ndz` at the distance `z` form the point P.
The magnetic field due to the circular loop is
`dB=(mu_0Ia^2)/(2(a^2+z^2)^(3/2))ndz`
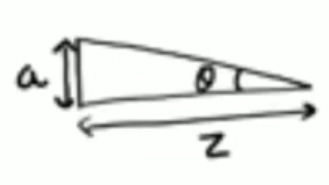
Let us express `dz` as `d theta`
`a/z=tan theta`
or, `z=a cot theta`
or, `dz=-a cosec^2 theta d theta`
and `a/sqrt(a^2+z^2)=sin theta`
or `sqrt(a^2+z^2)=a cosec theta`
The magnetic field due to the circular loop becomes,
`dB=(mu_0nIa^2)/2 1/(acosectheta)^3.(-acosec^2theta)d theta`
or, `dB=-(mu_0nI)/2sintheta d theta`
The magnetic field due to the solenoid is
`B=-int_(-theta_2)^(theta_1)(mu_0nI)/2sintheta d theta`
or, `B=(mu_0nI)/2[cos theta_1 -cos theta_2]`
We have `theta_1=0^circ`and `theta_2=180^circ`, The magnetic field becomes,
`B=mu_0nI`
Labels:
#Electrodynamics
#Physics
Share: