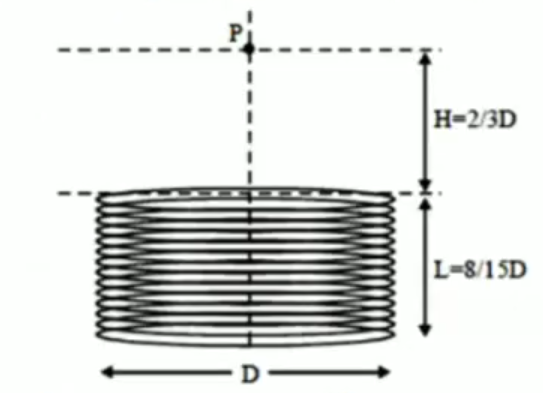
A short solenoid with in turns per unit length has diameter D and length `L = (8D )/ 15` as shown in the figure, and it carries a constant current I. The magnetic field B at a point P on the axis of the solenoid at a distance `H = (2D)/ 3` from its near end (see figure) is

A short solenoid with in turns per unit length has diameter D and length L = 8D / 15 as shown in the figure, and it carries a constant current I. The

Problem: A short solenoid with in turns per unit length has diameter D and length `L = (8D )/ 15` as shown in the figure, and it carries a constant current I. The magnetic field B at a point P on the axis of the solenoid at a distance `H = (2D)/ 3` from its near end (see figure) is [use integrate `int dx (1 + x ^ 2) ^ (- 3/2) = x(1 + x ^ 2) ^ (- 1/2) `]        [TIFR 2014]

✅(A) `4/65mu_0nI`    (B)`4/13mu_0nI`    (C)`24/15mu_0nI`    (D)`112/65mu_0nI`

Answer: 

The magnetic field at the point P due to the solenoid is given by 

`B=(mu_0nI)/2|[cos theta_1 -cos theta_2]|`

Note: 👉Click to see the calculation of the 'Magnetic of a solenoid'.

From the figure we get,

`cos theta_1=(2/3D)/sqrt((D/2)^2+(2/3D)^2)`

or, `costheta_1=4/5`

and `cos theta_2=(8/15D+2/3D)/sqrt((D/2)^2+(8/15D+2/3D)^2)`

or, `costheta_2=12/13`

Therefore the magnetic field at point P is 

`B=(mu_0nI)/2|[4/5-12/13]|`

or, `B=(4mu_0nI)/65`

Option A is correct.

Share:

Physics INK